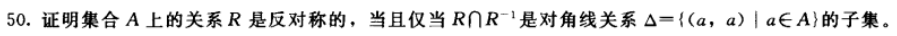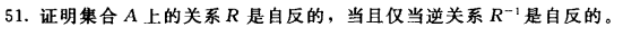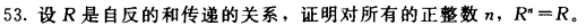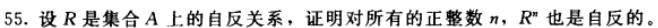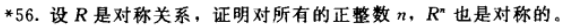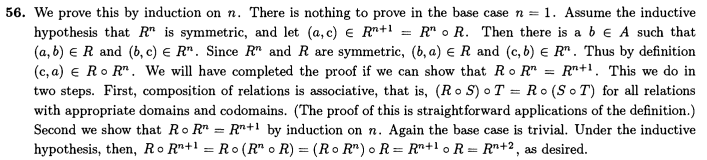7.1 关系及其性质 50 ~ 57

题目 50

解答 50

由“反对称”的定义可知，题目只是“反对称”的定义的另一种表达方式

题目 51

解答 51

如果R是自反的，则对于A的所有元素x，都有 $(x,x) \in R$ 。由于 ${R^{ - 1}}$ 是R的逆关系，所以 $(x,x) \in {R^{ - 1}}$ ，所以 ${R^{ - 1}}$ 是自反的。

如果 ${R^{ - 1}}$ 是自反的，则对于A的所有元素x，都有 $(x,x) \in {R^{ - 1}}$ 。由于R是 ${R^{ - 1}}$ 的逆关系，所以 $(x,x) \in R$ ，所以R是自反的。

题目 52

解答 52

因为R是集合A上的自反关系，所以对于A中的每一个元素x都有 $(x,x) \in R$ 。由于 $\overline R$ 是R的补关系，所以 $(x,x) \notin \overline R$ ，所以 $\overline R$ 是反自反的。

反过来，因为 $\overline R$ 是反自反的，所以对于A中的每一个元素x都有 $(x,x) \notin \overline R$ 。由于R是 $\overline R$ 的补关系，所以有 $(x,x) \in R$ ，所以R是自反的。

题目 53

解答 53

使用数学归纳法。

当n=1时，有 ${R^1}{\rm{ = }}R$ 。

对于任意正整数，因为R是传递的，由定理1，可知 ${R^{n + 1}} \subseteq R$ 。

要证 $R \subseteq {R^{n + 1}}$ 。由归纳假设 ${R^n}{\rm{ = }}R$ ，可知 ${R^{n + 1}} = {R^n} \circ R = R \circ R$ 。

取 $(a,b) \in R$ ，因为R是自反的，所以 $(b,b) \in R$ ，所以 $(a,b) \in R \circ R$ ，所以 $(a,b) \in {R^{n + 1}}$ ，从而 $R \subseteq {R^{n + 1}}$ 。

所以 $R = {R^{n + 1}}$ 。

综上所述，对于所有的正整数，都有 ${R^n}{\rm{ = }}R$

题目 54

解答 54

设题目中的集合为A

a)

除了(2,3)和(4,5)，包含 $A \times A$ 中所有其它元素。

b)

包含 $A \times A$ 中全部元素

c)

包含 $A \times A$ 中全部元素

d)

包含 $A \times A$ 中全部元素

题目 55

解答 55

用数学归纳法来证明。

当n=1时，有 ${R^1} = R$ ，显然成立。

假设 ${R^n}$ 是自反的，则对于所有的 $a \in R$ 都有 $(a,a) \in {R^n}$ 且 $(a,a) \in R$ ，所以 $(a,a) \in {R^n} \circ R = {R^{n + 1}}$ 。

所以对所有的正整数， ${R^n}$ 都是自反的。

题目 56

答案 56

解答 56

此题留着以后证。

题目 57

解答 57

不一定是。

假设集合A={1,3}，关系R={(3,1),(1,3)}，显然它是反自反的，但 ${R^2}$ ={(1,1),(3,3)}是自反的

(2013-01-08) 7.1 关系及其性质 50 ~ 57

题目 50

解答 50

题目 51

解答 51

题目 52

解答 52

题目 53

解答 53

题目 54

解答 54

a)

b)

c)

d)

题目 55

解答 55

题目 56

答案 56

解答 56

题目 57

解答 57