题目 01
解答 01
a) a等于b
{ (0,0), (1,1), (2,2), (3,3) }
b) a与b的和为4
{ (1,3), (2,2), (3,1), (4,0) }
c) a大于b
{ (1,0), (2,0), (2,1), (3,0), (3,1), (3,2), (4,0), (4,1), (4,2), (4,3) }
d) a整除b
a不可为0,b可为0.
{ (1,0), (1,1), (1,2), (1,3), (2,0), (2,2), (3,0), (4,0) }
e) a与b的最大公约数为1
gcd: greatest common divisor,最大公约数
定义:如果有一个自然数a能被自然数b整除,则称a为b的倍数,b为a的约数。几个自然数公有的约数,叫做这几个自然数的公约数。公约数中最大的一个公约数,称为这几个自然数的最大公约数。
在离散数学中,“自然数”包括0和正整数。
0与1的最大公约数为1。因为1的最大约数为1,它又能整除0。
{ (0,1), (1,0), (1,1), (1,2), (1,3), (2,1), (2,3), (3,1), (3,2), (4,1), (4,3) }
f) a与b的最小公倍数为2
lcm: Least Common Multiple,最小公倍数
{ (1,2), (2,1), (2,2) }
题目 02
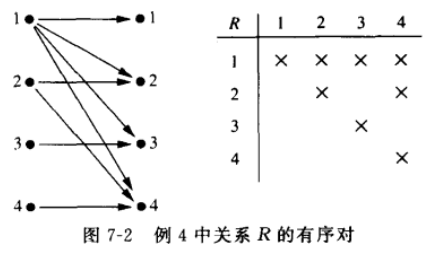
例4是什么样的
解答 02
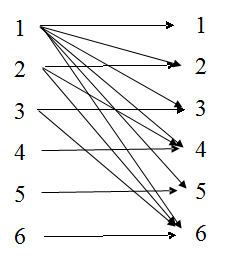
a) 集合表示法
{ (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,2), (2,4), (2,6), (3,3), (3,6), (4,4), (5,5), (6,6) }
b) 图表示法
c) 矩阵
| R | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | x | x | x | x | x | x |
| 2 | x | x | x | |||
| 3 | x | x | ||||
| 4 | x | |||||
| 5 | x | |||||
| 6 | x |
问题 03
解答 03
a)
- 自反 不是对称:有(2,4),没有(4,2) 不是反对称:因为存在对称点(2,3),(3,2) 传递*
b)
- 自反 对称 不是反对称*:因为存在对称点(1,2)与(2,1) 传递
c)
- 不是自反:缺少(1,1),(2,2),(3,3)和(4.4) 对称 不是反对称*:因为存在对称点(2,4)和(4,2) 不是传递:存在(2,4)和(4,2),但不存在(2,2)及(4,4)
d)
- 不是自反:缺少(1,1),(2,2),(3,3),(4,4) 不是对称:有(1,2),但没有(2,1) 反对称 不是传递*:有(1,2)和(2,3),但没有(1,3)
e)
- 自反 对称 反对称* 传递**
f)
- 不是自反:缺少(1,1)、(2,2)、(3,3)、(4,4) 不是对称:有(1,4),但没有(4,1) 不是反对称:存在对称点(1,3)和(3,1) 不是传递*:有(1,3)和(3,1),但没有(1,1)
问题 04
解答 04
a) a比b高
- 是“反对称”,“传递”* 不是“自反”,“对称”
b) a和b生在同一天
- 是“自反”,“对称”,“传递”* 不是“反对称”
c) a和b同名
- 是“自反”,“对称”,“传递”* 不是“反对称”
d) a和b有共同的祖父母
- 是“自反”,“对称”,“传递”* 不是“反对称”
问题 05
解答 05
a)
关键在于“每个”两字,可以理解为“所有”。
- 是自反的,因为访问了a的人也同时访问了a 不是对称的,因为不是每一个访问了b的人,都会访问a 不是反对称的,因为访问了(a,b)的人,有可能访问(b,a),也有可能不访问(b,a) 是传递*的,因为如果所有访问了a的人都访问了b,所有访问了b的人都访问了c,则所有访问了a的人都访问了c
b)
- 不是自反的,因为如果一个网页a上有链接,则a与a有公共链接,显然(a,a)不属于R 是对称的,因为a与b没有公共链接的话,则b与a必然没有公共链接 不是反对称的 不是传递*的,因为(a,b)没有公共链接,(b,a)也没有公共链接,但是(a,a)有公共链接
c)
是自反的,因为若a与b上至少有一条公共链接,则a与b上都至少有一条链接。a与a之间,也至少有一条公共链接,属于R如果某个网页a上没有链接,则“a与a至少有一条公共链接”不成立,则(a,a)不属于R,所以不是自反的。我之前误解了“自反”的概念。 是对称的,若a与b上至少有一条公共链接,则b与a上至少有一条公共链接 不是反对称的 不是传递*的,若(a,b)和(b,c)都属于R,但a与b的公共链接跟b与c的公共链接不相同,(a,c)有可能不属于R
d)
是自反的,若存在一个网页包含了到a与b的链接,则该网页包含到a与a的链接,即(a,a)属于R对于“所有网页来说”,对于某一个网页a来说,可能不存在一个网页包含了到它的链接,则(a,a)不存于R,所以不是自反的。我之前理解错了“自反”的定义。 是对称的,若存在一个网页包含了到a与b的链接,则必然包含了到b与a的链接,即(b,a)属于R 不是反对称的 不是传递*的,可能有一个网页包含了到a与b的链接,另一个网页包含了到b与c的链接,但没有网页包含到a与c的链接。
问题 06
解答 06
a) x+y=0
- (1,1)∉R,所以不是自反的 因为x+y=0,所以y+x=0,即(y,x)∈R,所以是对称的 因为存在对称点(x,y),且x≠y,所以R不是反对称的* 因为(1,-1)∈R,(-1,1)∈R,但(1,1)∉R,所以不是传递的
b) x=±y
- 因为(x,x)满足x=±y,所以是自反的 因为x=±y,所以y=±x,所以(y,x)∈R,所以是对称的 因为存在对称点(x,y),且x≠y,所以R不是反对称的* 若(x,y)∈R且(y,z)∈R,因为x=±y=±z,所以(x,z)∈R,所以是传递的
c) x-y是有理数
- 因为x-x=0是有理数,所以(x,x)∈R,所以R是自反的 如果x-y是有理数,则y-x=-(x-y)也是有理数,所以是对称的 因为存在对称点(x,y),且x≠y,所以R不是反对称的* 如果(x,y)∈R且(y,z)∈R,则x-y和y-z都是有理数,则它们的和(x-y+y-z)=x-z也是有理数,所以是传递的
d) x=2y
- (1,1)∉R,所以不是自反的 因为(4,2)∈R,但(2,4)∉R,所以不是对称的 若(x,y)∈R,则x=2y,则y=x/2。如果要让(y,x)∈R,则x/2=2x,只能x=0,则y=x=0。所以不是反对称的* 若(x,y)∈R且(y,z)∈R,则x=2y=4z,所以(x,z)∉R。所以不是传递的。
e) xy≥0
- 因为xx≥0,所以(x,x)∈R,所以是自反的 若(x,y)∈R,则yx=xy≥0,所以是对称的 因为(2,3)和(3,2)都属于R,所以R不是反对称的 因为(2,0)和(0,-1)属于R,但(2,-1)不属于R,所以不是传递的
f) xy=0
(1,1)不属于R,所以不是自反的 若(x,y)属于R,即xy=0,则yx=0,即(y,x)也属于R,所以是对称的 因为(4,0)和(0,4)都属于R,所以不是反对称的* 因为(4,0)和(0,4)都属于R,但(4,4)不属于R,所以R不是传递的
g) x=1
(2,2)不属于R,所以不是自反的 (1,2)属于R,但(2,1)不属于R,所以不是对称的 若(x,y)和(y,x)都属于R,则x=y=1,所以是反对称的* 若(x,y)和(y,z)都属于R,则x=y=z=1,所以R是传递的
h) x=1或y=1
- (2,2)不属于R,所以不是自反的 若(x,y)属于R,则x=1,所以(y,x)属于R,所以是对称的 因为(1,2)和(2,1)都属于R,所以不是反对称的* 因为(3,1)和(1,2)都属于R,但(3,2)不属于R,所以不是传递的
题目 07
解答 08
a) x≠y
- (1,1)∉R,所以不是自反的 则x不等于y,则y不等于x,所以是对称的 因为(2,3)和(3,2)都属于R,所以不是反对称的* 因为(2,3)和(3,2)都属于R,但(2,2)不属于R,所以不是传递的
b) xy≥1
显然R的域中不包含0,则xx大于等于1,则(x,x)属于R,所以是自反的0是整数,但(0,0)不满足xy≥1,所以(0,0)∈R,所以不是自反的 若xy大于等于1,则yx大于等于1,所以是对称的 因为(1,2)和(2,1)都属于R,所以不是反对称的 若xy大于等于1,且x,y都为整数,则x和y同号并且绝对值最小为1。若(x,y)和(y,z)都属于R,则x与y同号,y与z同号,所以x和z同号且最小值为1,所以x*z大于等于1,所以(x,z)也属于R。所以是传递的。
在做这个题的时候,我开始认为它是自反的,怎么都想不明白。后来在stackoverflow上网友的帮助下,才明白我对自反的概念理解错了。
自反的概念:A relation R on a set A is called reflexive if (a, a) ∈ R for every element a ∈ A,即对集合中所有的元素都有(a,a)属于R。
我之前理解成了,对于属于R的域中的每一个元素a都有(a,a)属于R。
这是提问:http://math.stackexchange.com/questions/271638/reloation-r-is-xy1-and-xz-and-yz-is-r-reflexive
从提问到得到答案只花了2分钟,太靠谱了!
c) x=y+1或x=y-1
- (1,1)不属于R,所以不是自反的 若(x,y)属于R,则x=y+1或y-1。则y=x-1或x+1,所以(y,x)也属于R。所以是对称的 因为(2,1)和(1,2)都属于R,所以不是反自反的* 因为(2,1)和(1,2)都属于R,但(2,2)不属于R,所以不是传递的
d) x≡y(mod 7)
- 因为x与x模7同余,所以是自反的 因为x与y模7同余,所以y与x模7同余,所以是对称的 因为(0,7)和(7,0)属于R,所以不是反对称的* 若(x,y)和(y,z)都属于R,则x=7k+y,y=7m+z,所以x=7(k+m)+z,所以x与z模7同余,所以是传递的
e) x是y的倍数
- 因为x是x的倍数,所以是自反的 因为(2,1)属于R,但(1,2)不属于R,所以不是对称的 因为(1,-1)和(-1,1)都属于R,所以不是反自反的 若(x,y)和(y,z)都属于R,则x=ky,y=mz,所以x=km*z,所以(x,z)也属于R,所以是传递的
f) x与y都是负的,或者都是非负的
- 显然(x,x)属于R,所以是自反的 如果(x,y)属于R,则x与y都是负数,或者都是非负数,所以yx也满足R,所以是对称的 因为(2,3)和(3,2)满足R,所以不是反对称的* 若(x,y)和(y,z)都属于R,则x、y、z都是负数,或者都是非负数,所以xz也满足R,所以是传递的
g) x=y^2
- (4,4)不属于R,所以不是自反的 (4,2)属于R,但(2,4)不属于R,所以不是对称的 若x是y的平方,且y是x的平方,则只能是x=y,所以是反对称的* (8,4)与(4,2)都属于R,但(8,2)不属于R,所以不是传递的
h) x≥y^2
- (4,4)不属于R,所以不是自反的 (4,2)属于R,但(2,4)不属于R,所以不是对称的 若(x,y)和(y,x)都属于R,则x≥yy≥xxxx,又因为x为整数,所以x=0或1,则y=x。所以是反对称的 若(x,y)和(y,z)都属于R,则x≥yy≥zzzz≥zz,所以(x,z)也属于R,所以是传递的
题目 08
解答 08
a)
如果一个关系既是对称的,又是反对称的,只有一种可能:如果有对称点,则对称点在矩阵的主对角线上。
假设集合A为{1,2,3,4},则{(1,1),(2,2),(3,3),(4,4)}的任一子集都是对称和反对称的。
b)
关系中既包含不相等的对称点,又包含没有对称点的点。
假设集合A为{1,2,3,4},则{(1,1),(2,1),(1,2),(2,3)},既不是对称的,也不是反对称的。
题目 09 ~ 12
解答 09 ~ 12
反自反比较好判断。只有当矩阵主对角线上全部为假时,即关系中不存在(a,a)这样的元素时,关系才是反自反的。
9.

其中,c、d、f是反自反的。
10

其中,a是反自反的。
11

四个都不是反自反的。
- a) 因为访问了某个网页a的人,当然也访问了网页a。所以不是反自反的。
- b) 若网页a上没有链接,则a与a上没有公共链接,属于R。所以不是反自反的。
- c) 如果网页a上有链接,则a和a上至少有一条公共链接,属于R。所以不是反自反的。
- d) 如果存在一个Web包含了到a的链接,则它包含了到a和a的链接,(a,a)属于R。所以不是反自反的。
12

全部都不是反自反的。
- 因为(0,0)属于R,所以不是反自反的
- 因为(0,0)属于R,所以不是反自反的
- 因为(0,0)属于R,所以不是反自反的
- 因为(0,0)属于R,所以不是反自反的
- 因为(0,0)属于R,所以不是反自反的
- 因为(0,0)属于R,所以不是反自反的
- 因为(1,1)属于R,所以不是反自反的
- 因为(1,1)属于R,所以不是反自反的